Kalkulus 2 Teknik Informatika

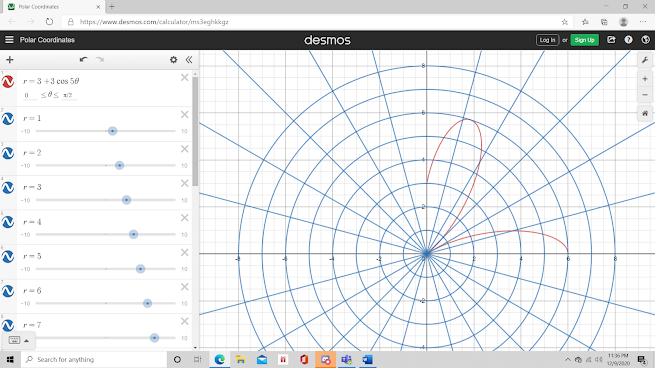
Nah, Untuk Pertemuan ini kita juga tidak melakukan meet karena ada nya kendala dalam waktu jadi kita mengerjakan Tugas Sebagai Presensi nyaa. Jadi, di Blog ini berisi tentang Soal yang diberi oleh Ibu nya dan cara pengerjaan nyaaa. Semoga Bermanfaat :) Tugas Mandiri Kalkulus Buat grafik dan hitung luas daerah dari fungsi berikut  1. ; 0 ≤ θ ≤ π/2 𝑟1=3+3cos5.0                     𝑟2=3+3cos5 .90° 𝑟1=3+3cos0                        𝑟2=3+3cos450° 𝑟1=3+3 .1                             𝑟2=3+3 ( −0.73 ) 𝑟1=3+3                                   𝑟2=3+(− 2.19 ) 𝑟1=6                                        𝑟2=−0.81 2. r= 2 cos θ + 4sin3 θ ; 0 ≤ θ ≤ π/2 𝑟1=2cos0+4sin3.0                          𝑟2=2cos90+4sin3.90 𝑟1=2 .1 + 4 . 0                                 𝑟2=2 (−0.44)+4 (−0.17) 𝑟1=2                                                     𝑟2=−0.88+(−0.68)                                                                𝑟2= −1.56 Demikian Pengerjaan yang saya kerjakan semoga bermanfaat

TUGAS MANDIRI PENGGANTI PRESENSI      Diblog kali ini karena pertemuan pada tanggal 29 Oktober 2020 tidak diadakan meet maka digantikan dengan membuat tugas untuk mengganti presensi maka di blog ini saya membuat Jawaban dari soal soal yang ada dalam Tugas pada pertemuan ini. Semoga Bermanfaat Sekian Jawaban Dari Soal yang ada untuk Tugas Mandiri Pengganti Presensi Pada Tanggal 29 Oktober 2020 Semoga Bermanfaat. Jikalau ada yang salah mohon dikoreksi di Kolom Coment nyaaa yaa Guyss! Semangattt!  

V olume yang dihasilkan dari sebuah luasan yang diputar dengan poros putar tertentu (sumbu x / sumbu y). Salah satu bentuk pengaplikasian integral selain menghitung luas di bawah kurva juga untuk menghitung volume pada benda putar. Contoh paling sederhana dari benda putar yaitu tabung. Volume sebuah tabung didapatkan dari luas alas berbentuk lingkaran yang dikalikan tinggi. Volume Benda Putar Jika alas tabung yang dinyatakan dengan fungsi A(x) dan tinggi dari benda putar itu adalah panjang selang dari titik a ke b pada sumbu x atau y maka volume benda putar itu bisa dihitung dengan memakai rumus Rumus Volume Benda Berputar a. Volume Benda Putar Sumbu x yang dibatasi 1 Kurva perhatikan gambar di atas. Luasan di bawah kurva y=f(x) jika diputar dengan sumbu putar dengan titik batas a dan b mampu menghasilkan sebuah silinder tinggi selisih b dan a. Volume benda putar menurut sumbu x diatas bisa dicari memakai rumus b. Volume Benda Putar Sumbu y yang dibatasi 1 Kurva Volume benda putar deng

       Sistem Koordinat merupakan sebuah sistem untuk menentukan suatu titik dalam ruang n-dimensi. Sistem untuk satu-dimensi dinamakan dengan sistem garis bilangan, yaitudigunakan untuk menentukan posisi suatu bilangan. Sistem untuk dua-dimensi dinamikan dengan bidang datar, digunakan untuk menentukan pasangan dua titik (a,b). Sistem Koordinat Polar termasuk dalam sistem yang digunakan untuk meneniukan posisi suatu titik dalam bidang datar.      Koordinat Polar dibangun dengan menggunakan dua acuan, yaitu: satu titik pusat (pole) dan satu sumbu Kutub yang berupa garis mendatar dari titik pusat (x-ray) ke arah kanan. Suatu titik dalam Bidang polar disajikan dalam P(r,Teta) dengan r menyatak'an jaiak bertanda (assigned distance ) dari titik pusat ke titik P, dan Teta menyatakan besarnya sudut yang diukur dari sumbu Kutub ke arah sumbu yang menghubungkan titik pusat dengan titik p. Sudut Teta bernilai positif jika diukur berlawanan arah dengan perputaran jarum jam, dan bernilai negat

Bentuk umum fungsi dalam koordinat polar adalah r = f(Teta), Misalnya  r = sin(Teta). Daerah definisi fungsi dalam koordinat polar ditentukan dengan berpedoman bahwa Teta harus sedemikian besarnya sehingga memberikan r yang berharga nol atau positip. Grafik Fungsi dalam koordinat polar diperoleh dengan cara menghubungkan titik-titik P(r,Teta) dengan Teta berasal dari daerah definisi.  Macam grafik dalam koordinat Polar : Garis Garis dalam koordinat kutub dapat dinyatakan sebagai berikut: Garis vertikal yang melalui (a, 0):  r cos θ = a Garis horisontal yang melalui (0, b):  r sin θ = b Garis yang melalui (0, 0):  θ = θ 0 Contoh : Lingkaran Beberapa persamaan lingkaran dapat dinyatakan dalam koordinat kutub. Lingkaran berjari-jari a dengan pusat (0, 0):  r = a Lingkaran berjari-jari a dengan pusat (a, 0):  r = 2a cos θ Lingkaran berjari-jari a dengan pusat (0, a):  r = 2a sin θ Contoh :

Volume Benda Pejal      Banyak besaran dapat dianggap sebagai hasil pengirisan sesuatu menjadi potongan-potongan kecil, aproksimasi, tiap potongan, penjumlahan dan pengambilan limit  ketika tiap potongan ukurannya mengecil. Metode tersebut dapat diterapkan un tuk mencari volume benda pejal asalkan volume masing-masing potongan mudah diaproksimasi.      Benda putar yang sederhana dapat kita ambil contoh adalah tabung dengan besar volume adalah hasilkali luas alas ( luas lingkaran ) dan tinggi tabung. Volume dari benda putar secara umum dapat dihitung dari hasilkali antara luas alas dan tinggi. Bila luas alas kita nyatakan dengan A(x) dan tinggi benda putar adalah panjang selang [ a,b ] maka volume benda putar dapat dihitung menggunakan integral tentu sebagai berikut :  Untuk mendapatkan volume benda putar yang terjadi karena suatu daerah diputar terhadap suatu sumbu, dilakukan dengan menggunakan dua buah metode yaitu metode cakram dan kulit tabung. Volume Benda Pejal di Ruang; Metode Ci

Luas Daerah      Luas Daerah yang dibatasi oleh beberapa kurva dapat ditentukan dengan menghitung integral tertentu. Andaikan kurva y = f(x) dan kurva y = g(x) kontinu pada interval a ≤ x ≤ b, dan kurva y = f(x) terletak di atas atau pada kurva y = g(x), maka luas daerah yang dibatasi kurva  y = f(x), kurva y = g(x), garis x = a Dan  x = b adalah sebagai berikut: Langkah-langkah Menghitung Luas Daerah : 1. Tentukan daerah yang diminta dengan menggambardaerahnya 2. Perhatikan daerah yang dimaksud untuk menentukan batas-batas integrasinya               3. Tentukan rumus luasyang lebih mudah digunakan (L = ∫ y dx atau L = ∫ x dy ) 4. Hitung nilai integral sebagai hasil luas daerah

Integral Tentu Integral tentu adalah integral yang memiliki nilai batas atas dan batas bawah. Batas-batas yang diberikan umumnya adalah suatu nilai konstanta. Namun dapat juga batas-batas tersebut berupa variabel. Untuk mencari nilai integral tertentu dari suatu fungsi, pertama kita substitusikan batas atas ke dalam fungsi hasil integral, kemudian dikurangi hasil substitusi batas bawah pada fungsi hasil integral. Rumus Integral Tentu : Keterangan: f(x) = fungsi yang nantinya akan kita integralkan d(x) = variabel integral a = batas bawah pada variabel integral b = batas atas pada variabel integral F(a) = nilai integral pada batas bawah F(b) = nilai integral pada batas atas Dari rumus di atas, terdapat beberapa sifat integral tentu yang wajib kamu tahu. Sifat integral tentu ini bakalan ngebantuin kamu buat nyederhanain persoalan yang lagi kamu kerjain. Berikut beberapa sifat integral tentu. Contoh Soal : 1.  Hitunglah hasil dari integral tentu berikut ini          Jawab : 

Dalam mendefinisikan integral tentu sebagai limit jumlah Reimann ada dua syarat yang harus dipenuhi, yaitu : a. Batas pengintegralan berhingga b. Integran(f(x)) berhingga pada selang [a,b]  Jika paling kurang salah satu syarat diatas tidak dipenuhi maka integral tentu disebut integral tak wajar Jenis-jenis integral tak wajar : a. Integral tak wajar dengan batas pengintegralan tak hingga       Setiap bilangan asli merupakan bilangan terhingga dan dapat menyatakan sesuatu yang banyaknya terhingga.karena bilangan asli n +1 atau 2n lebih dari n , yang juga merupakan bilangan terhingga. Lambang teta memang bukan untuk menyatakan suatu bilangan, karena ketakterhinggaan aktual tidak ada dan yang ada hanyalah ketakterhinggan potensial. Bilangan n berapapun tidak akan mampu menjelaskan berapa banyak bilangan asli. Dengan demikian, jumlah berapa banyak bilangan asli adalah tak terhingga. b. Integral tak wajar dengan integran tak hingga      Pada kasus sebelumnya, integral tentu yang telah dipela